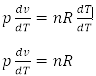Thermodynamics System
a) Open system
b) Closed System
c) Isolated System
Thermodynamics Process
1) Isothermal Process
2) Isochoric process
3) Isobaric process
The process in which pressure remains constant is called the isobaric process.
4) Adiabatic process
The process in which pressure, volume, and temperature change but the amount of heat remain constant is called the adiabatic process.
Work done by expansion

Fig: Work done by expansion
Let us consider a gas kept inside a cylinder provided with a movable and frictionless piston at pressure 'p', volume 'v', and temperature 'T'. Suppose the gas expands by a small volume 'dv' and the piston moved forward by distance 'dx'. If A is the cross-sectional area of the cylinder then force on the piston,
F = P.A [∴ P=F/A]
Also, the change in volume
dv = Adx
Now,
dw= F.dx
dw= PAdx
dw= Pdv
which is external work done
PV diagram
Internal energy
For Ideal gas, Internal energy = kinetic energy
First Law of thermodynamics
It states that if a certain amount of heat is supplied to the given system then a part of the heat may be used to increase the internal energy and the remaining part is used for work done.
If dQ is the amount of heat supplied to the system and du, dw is the increases in internal energy and external work done respectively, then according to the first law of thermodynamics.
dQ = du + dw --- (i)
since
dQ = du + pdv
If dv = 0 then dw = 0
∴ dQ = du
It means the total amount of heat supplied is used to increase external work done only when the volume is constant.
Heat Capacity of gas
Molar heat as constant volume (Cv)
It is defined as the amount of heat required to rise the temperature of 1 mole of gas through 1 kelvin at constant volume. It is denoted by Cv.
Molar heat as constant pressure (Cp)
It is defined as the amount of heat required to rise the temperature of 1 mole of gas through 1 kelvin at constant pressure. It is denoted by Cp.
Mayer's formula (Cp-Cv=R)
Let us consider 'n' mole of gas kept in a cylinder provided with the movable and frictionless piston at pressure 'P', volume 'V', and Temperature 'T'. Suppose the gas is heated at constant volume initially and dQ is the amount of heat given to the system to increase its temperature by dT then,
dQ = nCvdT --- (i)
From the first law of thermodynamics,
dQ = du + PdV
Since, at constant volume, dv=0
so, dQ = du
∴ du = nCv dT --- (ii)
Again the gas is heated at constant pressure and dQ be the amount of heat given to the system to increase the temperature by dT.
dQ = nCpdT --- (iii)
Again from first law of thermodynamics
dQ = du + Pdv
nCpdT = nCvdT + Pdv---(iv) ∴using equation (ii)
From idea gas equation
PV = nRT
Differentiating both sides with respect to at T at constant pressure.
Equation of Adiabatic Process
From the first law of thermodynamics
dQ = du + pdv --- (i)
For adiabatic process
dQ = 0 (∴ heat constant)
du + Pdv = 0 --- (ii)
If Cv is the molar heat capacity at a constant volume for one mole of gas,
du = 1Cvdt --- (iii)
using equation (iii) in equation (ii)
CvdT + Pdv = 0 --- (iv)
Also ideal gas equation for 1 mole of gas
PV = RT
Differentiating both sides with respect to 'T'
P dv / dT + V dP / dT = R dT / dT
P dv + vdP = R dT
dT = Pdv + Vdp / R --- (v)
using equation (v) in equation (iv)
Cv ( Pdv + Vdp / R ) + Pdv = 0
Cv (Pdv + Vdp) + RPdv = 0
(CV+R) Pdv + CvVdp = 0 [ ∴ cp-cv=R]
CpPdv + CvVdp = 0
Dividing both side by CvPv
Integrating on both sides
In terms of pressure and volume
In terms of temperature and volume
We have,
In terms of pressure and temperature
Work done by an isothermal process
dw = PdV --- (i)
Thus total work done
for 1 mole of the gas ideal gas equation be,
PV = RT
P = RT / V --- (iii)
using equation (iii) in equation (ii)
Work done by Adiabatic process
For one mole of gas
Equations (iv) and (iii) are required expressions for n mole of gas during the adiabatic Process.
Reversible and Irreversible Process
If you want to ask anything, please contact us by Messaging us on Social Media.
Second Law Of Thermodynamics
1) Kelin's Statements
2) Clausius Statements
It is impossible to make flow to heat from the body at a lower temperature to the body at a higher temperature without any external work done.
Heat Engine
A heat engine is a device that converts heat energy into mechanical work. It consisted of three parts they are:-
1) Source
2) Working Substance
Working Substance is an ideal gas that on being supplied with heat performs mechanical work.
3) Sink
The efficiency of Heat Engine

Fig: Heat engine
The efficiency of a heat engine is defined as the ratio of the amount of work done to the total heat taken from the source.
If, Q1 is the amount of heat taken from the source and Q2 is the heat rejected to sink.
Then work done (Q) = Q1 - Q2

No engine will convert all the heat absorbed from the source into work. So, the efficiency of an engine is always less than 1 or 100%.
Refrigerator
A refrigerator is a device that transfers heat from a cold body to a heat body by means of an external agency.

Let Q be the amount of heat taken from the body at a lower temperature and W be the work done on it. So, that amount of heat absorbed by the hot body is,

Co-Efficient of Performance of a Refrigerator

Relation between co-efficient of performance and efficiency
for a heat engine working between Q1 and Q2 is,

and for refrigerator working between Q1 and Q2 is,

From equation (i)

using equation (iii) in Equation (ii)

This is a required relationship between the coefficient of performance and efficiency.
Carnot engine
Carnot performs an ideal heat engine having maximum efficiency which can work in a cycle of operation is called Carnot engine.
Carnot cycle
The Carnot engine performs work in four-cycle of operations having two isothermal and two adiabatic processes such a cycle of operation is called the Carnot cycle.
Consider a mole of an ideal gas enclosed in a cylinder having initial pressure, volume, and temperature P1, V1, and T1 respectively. The point corresponding to this pressure, volume and temperature are A in the PV diagram as shown in the figure. The different processes in a Carnot cycle are discussed below.

Fig: PV - diagram of the Carnot cycle
(I) Isothermal expansion
Initially, the cylinder is placed on a hot source, and gas absorbed a Q1 amount of heat at a constant temperature, and gas is expanded isothermally from initial state A(P1, V1) to final state B(V1, V2) which is represented by curve AB in a PV-diagram.

(II) Adiabatic expansion
Now, the cylinder is kept on an insulating stand, and gas is expanded adiabatically from the initial state is B(P2, V2) to C(P3, V3), and temperature changes from T 1 to T2 which is shown by curve BC in PV-diagram.

(III) Isothermal compression
Now, the engine is placed on a sink and is compressed isothermally from initial state C(P3, V3) to D(P4, V4) at constant temperature T2 which is shown by curve CD in PV-diagram. At this stage, an amount of heat is rejected to sink.

Adiabatic compression
Now, the cylinder is kept on an insulating stand and compressed the gas adiabatically from D(P4, V4) to A(P1, V1) which is shown by curve DA in PV-diagram and temperature change from T2 toT1.

Therefore the total amount of work done during one complete cycle; is,

Hence in the Carnot engine, net work done by the gas per cycle is numerically equal to the total area of the loop ABCDA representing the cycle.
The efficiency of the Carnot cycle
It is defined as the radius of external work done (w) by the engine to the amount of heat energy (Q1) absorbed from the heat source.


From the adiabatic curve BC
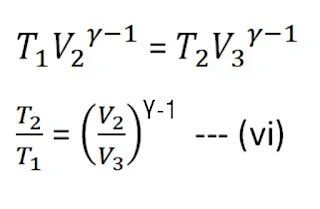
Again from the adiabatic curve DA

From equations (vi) and (vii)
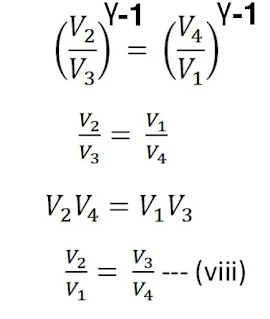
using equation (viii) in equation (v) , we get

This is a required expression for the efficiency of the Carnot engine
Petrol engine
A Petrol engine is developed by otto which consists of a cylinder fitted with a moveable piston. There are two holes in the cylinder fitted with inlet value ( I ) and outlet value ( v ). The opening and closing of those values are controlled by the motion of the piston. A spark plug 'S' produces a spark that ignites the mixture of air and Petrol (98-1. air and 2.). Petrol). The Piston is attached to the rod R which is connected to the wheels of vehicles. The Petrol engine works in the following four steps.

Fig: Four-stroke of a petrol engine

Fig:- PV diagram of a petrol engine
I. Suction Stroke:
It is shown in figure (a). In this Stroke the inlet valve 'I' opens and a mixture of oil and petrol is sucked into the cylinder by the outward motion of the piston which is shown by curve EA.
II. Compression Stroke:
It is shown in figure (b). In this stroke the inlet and outlet valve are closed. The mixture of air and petrol is compressed adiabatically 1/5 of original volume hence the temperature rise up to 600 ℃ which is shown by curve AB in PV diagram.
III. Working Stroke:
It is shown in figure (c). In this stroke, both the inlet and outlet valve are closed and a spark is produced from the spark plug 's' hence the temperature rises about 200 ℃ and hence pressure also rises up to 15 atmospheres which are shown by curve BC in the PV diagram and in this stage Q1 amount of heat is supplied. After ignition, the piston is pushed outward so the wheels rotate due to which temperature and pressure fall down which is shown by curve CD.
IV. Exhaust Stroke:
It is shown in figure (d). In this stroke, the outlet valve 'O' opens hence the burn gas escape out and the pressure falls which is shown by curve DA in the PV diagram.
Efficiency


Diesel engine
The diesel engine is developed by Rudolf Diesel and consists of a cylinder fitted with an inlet valve (I), outlet valve (E), and oil spray (O). The piston of the diesel engine is connected to the wheel through the rod 'R'. The working of the diesel engine was completed in 4 steps.
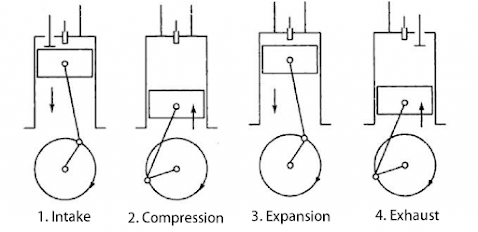
Fig:- Four-stroke of a diesel engine

I. Suction stroke
It is shown in figure (a) In this stroke inlet; the valve is open and air enters inside the cylinder by the outward movement of the piston. This is shown by Curve CA in the PV diagram.
II. Compression stroke
It is shown in figure (b) In this stroke. all the values are closed and the air is compressed adiabatically 1/17th of its original volume and the temperature inside the cylinder rises up to 100℃ which is shown by curve AB in the PV diagram.
III. Working Stroke
It is shown in figure (c). In this stroke, the oil spray valve 'O' opens and diesel enters inside the chamber where diesel burns and the volume rises at constant pressure which is shown by curve BC in PV-diagram. The work is done in this stroke. when the temperature inside the chamber reaches 2000°C; and the value O is closed. Now the volume increases due to high temperature and low pressure which is shown by the curve CD in the PV diagram.
IV. Exhaust Stroke
It is shown in figure (d). In this Stroke pressure decreases at constant volume hence a burning gas will escape out from the outlet valve which is shown by curve DA in PV-diagram and the next cycle begins.
Efficiency